Práctica 4: Regresión

Author

Aritz Adin

Published

11/11/2024

1. Regresión

1.1. Emplea el fichero bloodpress1.txt para ajustar un modelo de regresión lineal que permita estimar la presión sistólica en hombres según la edad.

datos <- read.table("bloodpres1.txt", header=TRUE)
head(datos)
  sbp age sex
1 158  41   M
2 185  60   M
3 152  41   M
4 159  47   M
5 176  66   M
6 156  47   M
  • Seleccionamos los hombres, representamos un diagrama de dispersión y ajustamos un modelo de regresión lineal con la función lm()
pos <- which(datos$sex=="M")
datos.male <- datos[pos,]

## Diagrama de dispersión ##
plot(datos.male$age, datos.male$sbp)

## Covarianza y correlación ##
cov(datos.male$age, datos.male$sbp)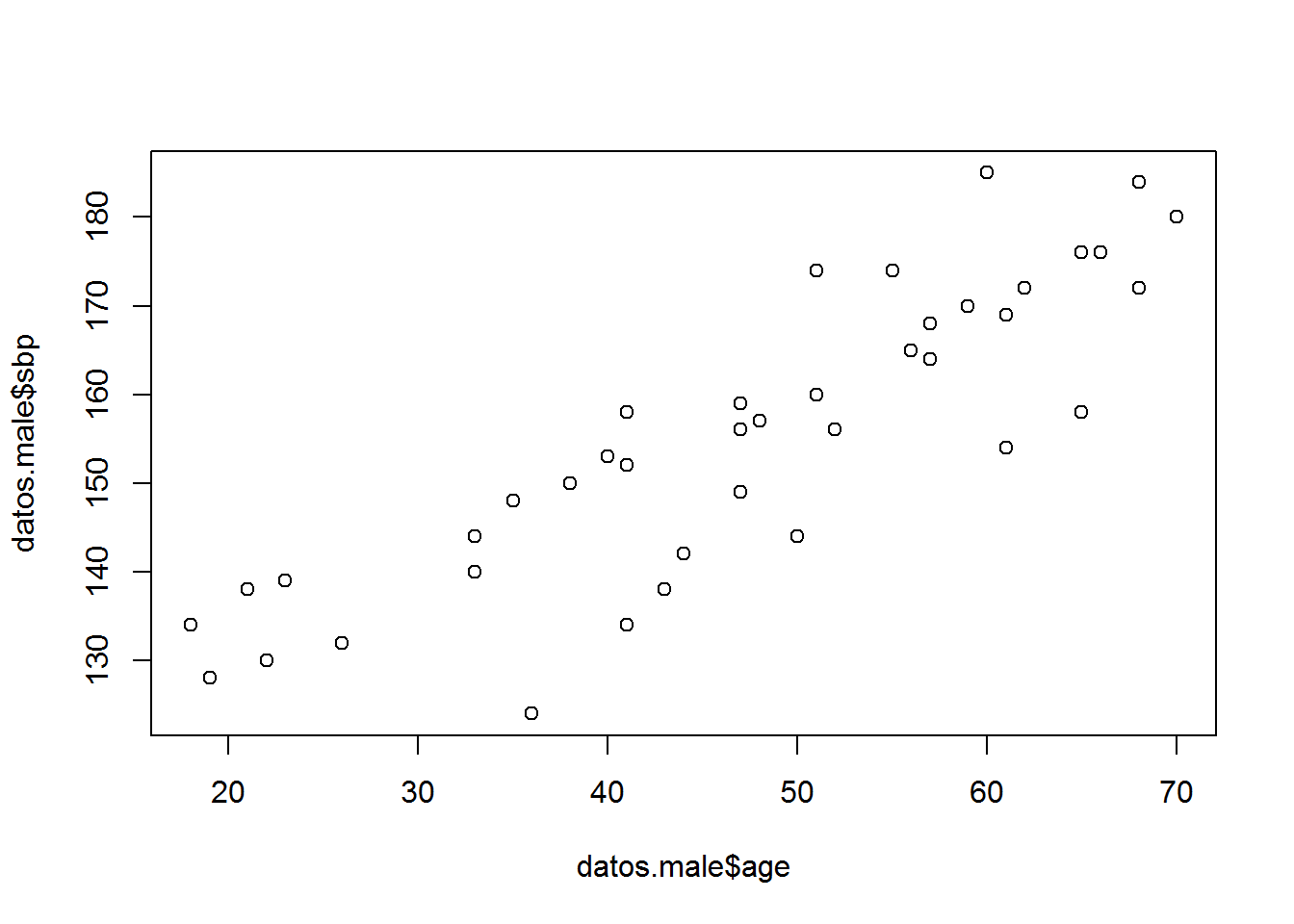
[1] 212.6013
cor(datos.male$age, datos.male$sbp)
[1] 0.8629821
## Modelo de regresión lineal ##
model.male <- lm(sbp~age, data=datos.male)
  • Proporciona una interpretación para los coeficientes
summary(model.male)

Call:
lm(formula = sbp ~ age, data = datos.male)

Residuals:
    Min      1Q  Median      3Q     Max 
-20.647  -3.128   1.681   3.912  17.280 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 110.0385     4.4892   24.51  < 2e-16 ***
age           0.9614     0.0913   10.53 7.98e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.479 on 38 degrees of freedom
Multiple R-squared:  0.7447,    Adjusted R-squared:  0.738 
F-statistic: 110.9 on 1 and 38 DF,  p-value: 7.985e-13

  • \(\beta_0=110.0385\) mmHg: Valor esperado para un hombre de 0 años de edad (en este ejemplo, no tiene sentido)

  • \(\beta_1=0.9614\): Por cada año que aumenta la edad de un hombre, se espera que la presión sistólica aumente en 0.9614 mmHg.

  • Representa gráficamente la línea ajustada

plot(datos.male$age, datos.male$sbp)
abline(model.male, col="red", lwd=2)

  • Verifica que se cumplen las hipótesis del modelo
library(PASWR2)
Cargando paquete requerido: lattice
Cargando paquete requerido: ggplot2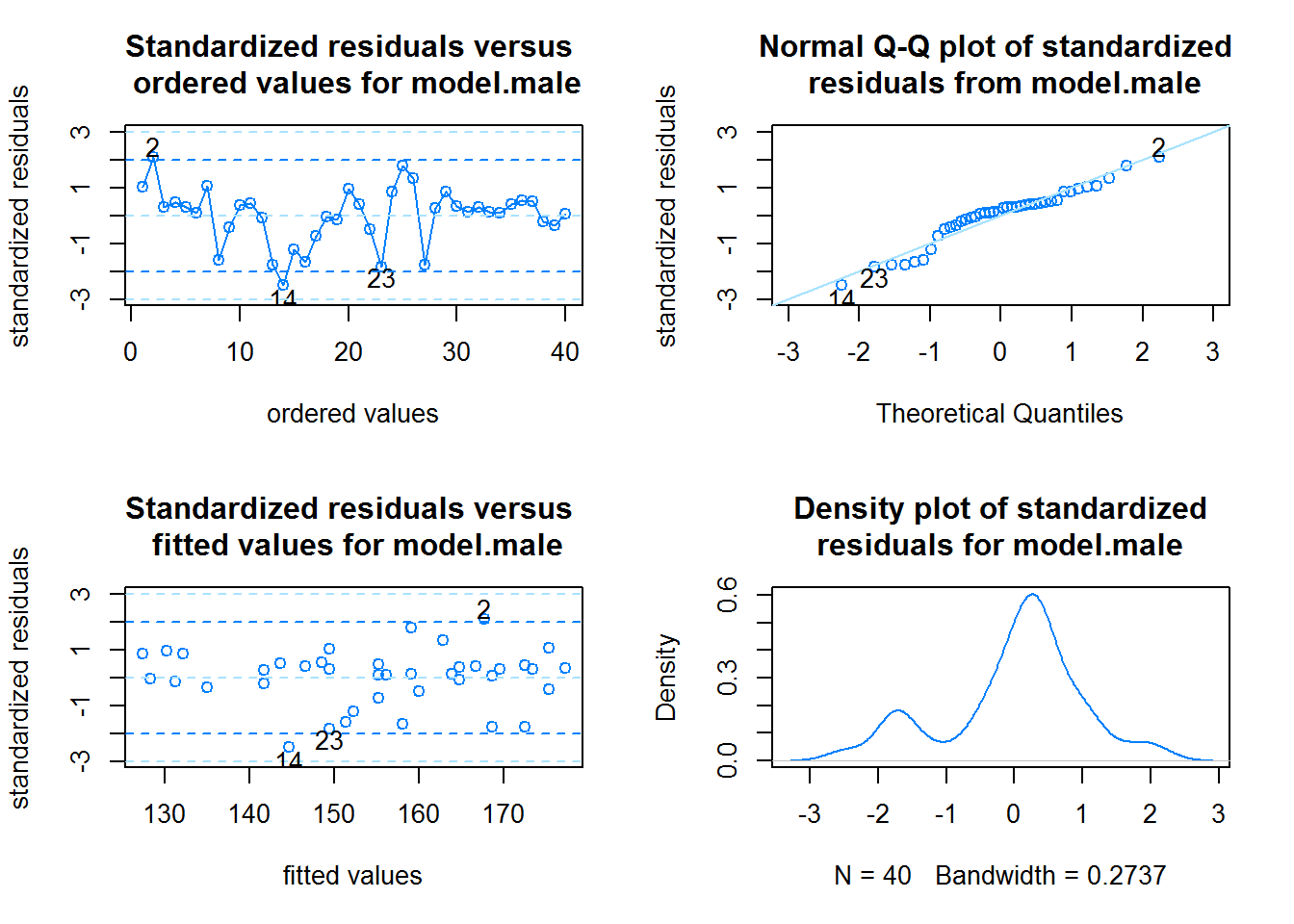
checking.plots(model.male)

res <- rstandard(model.male)
shapiro.test(res)

    Shapiro-Wilk normality test

data:  res
W = 0.93985, p-value = 0.03418

Aunque no se verifica la hipótesis de normalidad de los residuos (p-valor\(<0.05\)), pero seguiremos con el ejercicio.

  • Obtén la predicción para cinco hombres de 20, 29, 46, 58 y 65 años de edad
newdata <- data.frame(age=c(20,29,46,58,65))

predictions <- predict(model.male, newdata, interval="prediction")
predictions
       fit      lwr      upr
1 129.2656 111.1885 147.3426
2 137.9178 120.2262 155.6093
3 154.2607 136.8814 171.6401
4 165.7970 148.2983 183.2956
5 172.5264 154.8297 190.2232

1.2. Emplea el fichero bloodpress1.txt para ajustar un modelo de regresión lineal que permita estimar la presión sistólica en mujeres según la edad.

  • Seleccionamos los hombres, representamos un diagrama de dispersión y ajustamos un modelo de regresión lineal con la función lm()
pos <- which(datos$sex=="F")
datos.female <- datos[pos,]

## Diagrama de dispersión ##
plot(datos.female$age, datos.female$sbp)

## Covarianza y correlación ##
cov(datos.female$age, datos.female$sbp)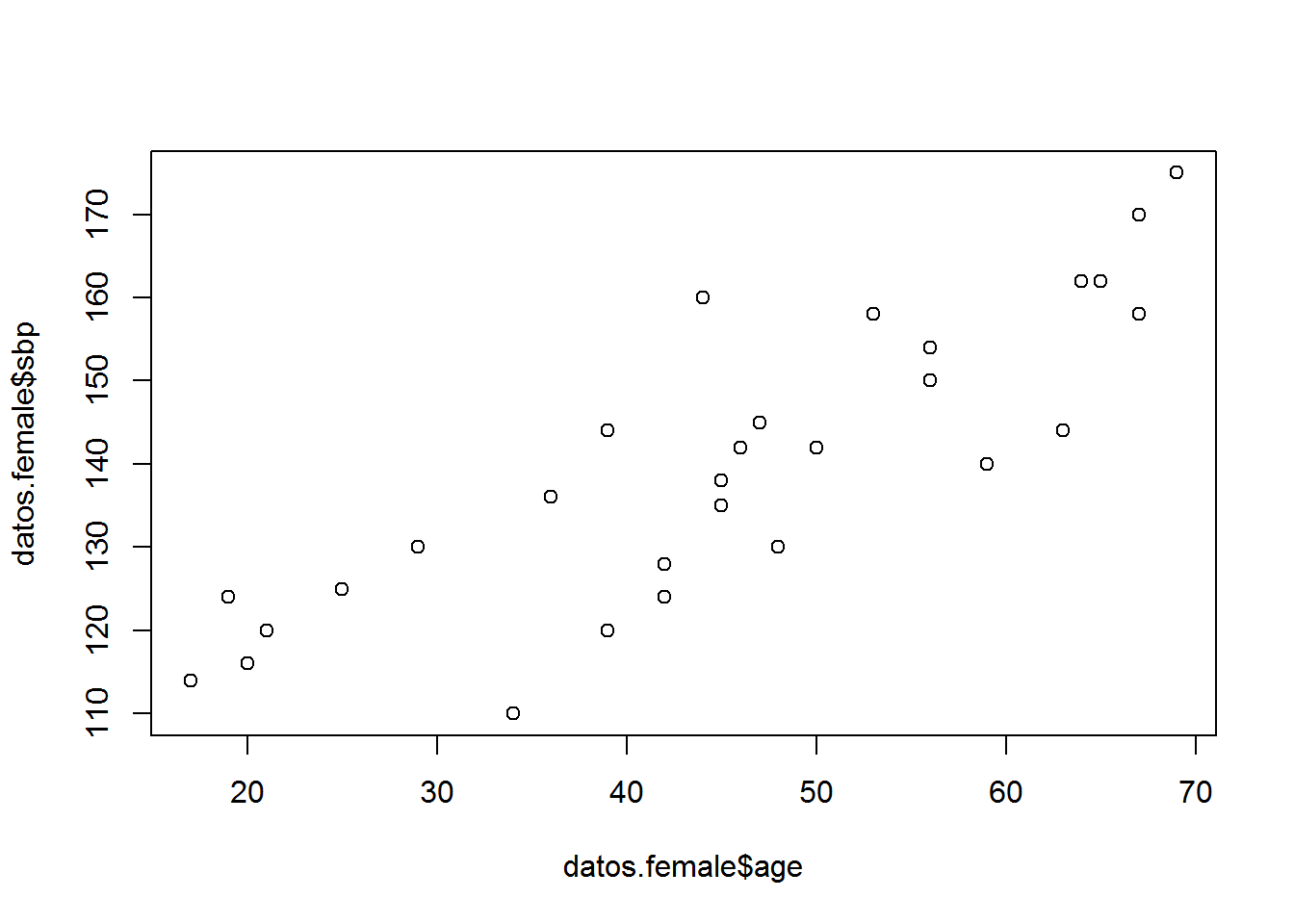
[1] 229.867
cor(datos.female$age, datos.female$sbp)
[1] 0.8439069
## Modelo de regresión lineal ##
model.female <- lm(sbp~age, data=datos.female)
  • Proporciona una interpretación para los coeficientes
summary(model.female)

Call:
lm(formula = sbp ~ age, data = datos.female)

Residuals:
    Min      1Q  Median      3Q     Max 
-19.354  -4.797   1.254   4.747  21.153 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  97.0771     5.5276  17.562 2.67e-16 ***
age           0.9493     0.1161   8.174 8.88e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.563 on 27 degrees of freedom
Multiple R-squared:  0.7122,    Adjusted R-squared:  0.7015 
F-statistic: 66.81 on 1 and 27 DF,  p-value: 8.876e-09

  • \(\beta_0=97.0771\) mmHg: Valor esperado para una mujer de 0 años de edad (en este ejemplo, no tiene sentido)

  • \(\beta_1=0.9493\): Por cada año que aumenta la edad de una mujer, se espera que la presión sistólica aumente en 0.9493 mmHg.

  • Representa gráficamente la línea ajustada

plot(datos.female$age, datos.female$sbp)
abline(model.female, col="red", lwd=2)

  • Verifica que se cumplen las hipótesis del modelo
library(PASWR2)
checking.plots(model.female)

res <- rstandard(model.female)
shapiro.test(res)

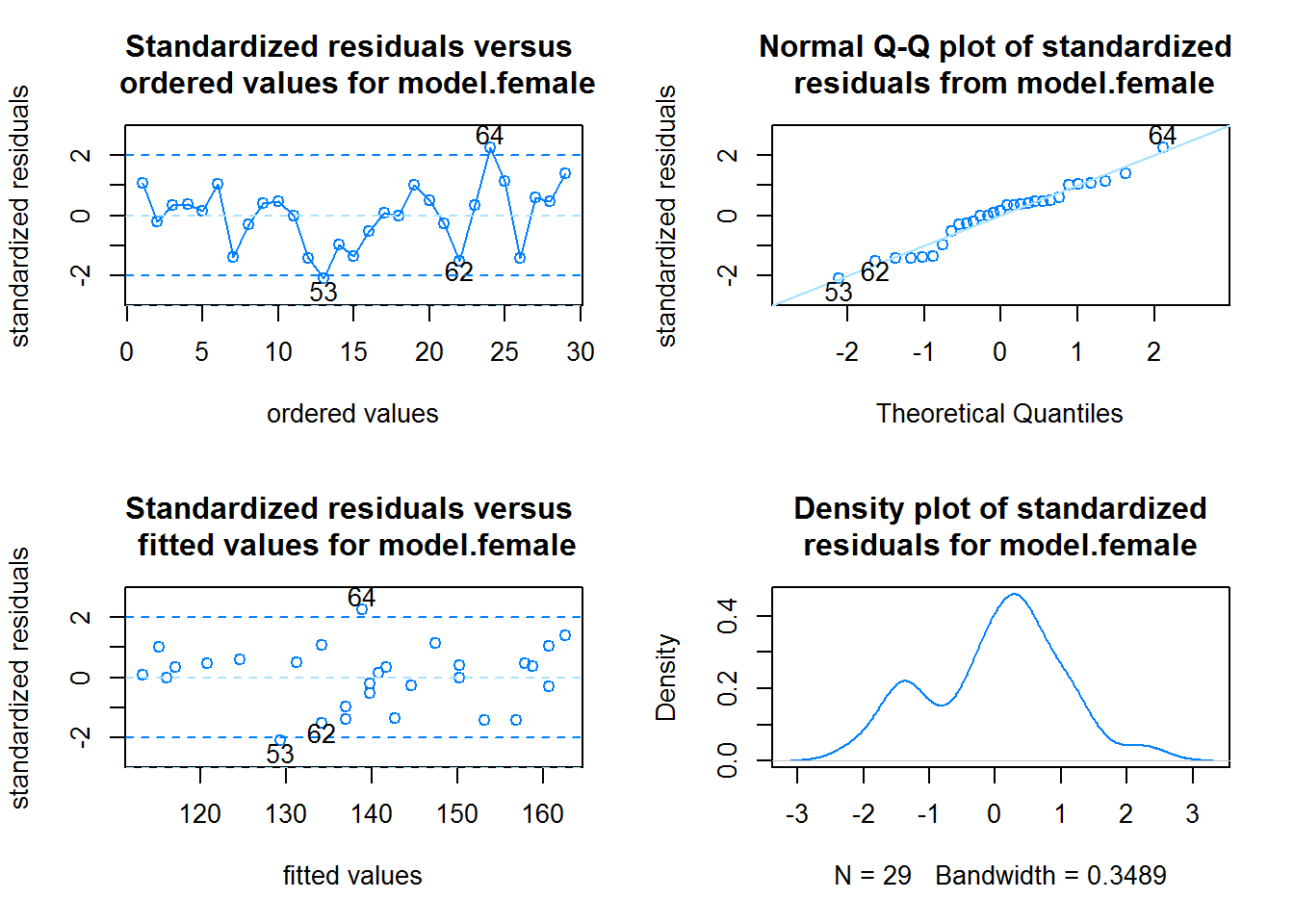
    Shapiro-Wilk normality test

data:  res
W = 0.96328, p-value = 0.3948
  • Obtén la predicción para cinco mujeres de 23, 26, 32, 55 y 62 años de edad
newdata <- data.frame(age=c(23,26,32,55,62))

predictions <- predict(model.female, newdata, interval="prediction")
predictions
       fit      lwr      upr
1 118.9115  98.2724 139.5506
2 121.7595 101.2909 142.2281
3 127.4554 107.2561 147.6547
4 149.2898 129.1922 169.3874
5 155.9351 135.5735 176.2966

2. Para entregar

2.1. Con el fichero HSWRESTLER de la librería PASWR2, ajusta un modelo de regresión para predecir la cantidad de grasa (tanfat). Selecciona las variables age, ht, wt, abs, triceps y subscap que mejor sirvan para predecir los valores de tanfat.

  • Selecciona las variables eliminado secuencialmente aquellas que no son estadísticamente significativas.

  • Utiliza también la función stepAIC() de la librería MASS para seleccionar las variables.

  • Interpreta los coeficientes del modelo.

  • Predice el valor de tanfat para dos individuo con valores de la variable abs de 20mm y 25mm, respectivamente, y valores de subscap de 13mm.